
Version française
Recherche
post-doc
thèse : travaux
thèse : résumé
références biblio
Enseignement
Publications
CV
English version
Ces travaux ont été réalisés en collaboration avec le laboratoire IUSTI, au département de Mécanique Énergétique de Polytech'Marseille, et dirigés par le Professeur Jean-Claude LORAUD.
Il existe beaucoup de modèles ayant conduit à des codes de simulation infrarouge (parmi lesquels SHIPIR [VF99], PRISM [SR88], ou SensorVision [DW01]), produisant des images à des résolutions très diverses, allant du kilomètre à une échelle inférieure au mètre. Les modèles thermiques présents dans ces simulateurs considèrent tous des transferts monodimensionnels (1D) : ils ne prennent pas en compte les transferts thermiques latéraux et se limitent à modéliser les flux conductifs dans le sens vertical. Si à grande échelle l'hypothèse 1D est vérifiée, ce n'est plus le cas à une échelle inférieure au mètre : les simulateurs ne sont pas capables de restituer correctement les variations spatiales des températures de surface. Des modèles 3D peuvent rendre compte de ces variations, mais le temps de calcul qui leur est nécessaire est prohibitif.
Mon travail de thèse se proposait donc d'améliorer la représentation en température d'une surface avec relief, d'abord en identifiant les origines de la variabilité spatiale et temporelle de la température de surface pour des sols avec relief, puis en proposant des approches physiques simples 1D afin de la modéliser.
Pour cela, la démarche que j'ai suivie dans ce travail a comporté trois étapes :
- expérimentale : effectuer des mesures de température de surface sur une géométrie complexe, pour mieux comprendre quels phénomènes influent principalement sur la variabilité de la température ;
- numérique : valider un code de référence, pour disposer d'un modèle permettant de simuler plusieurs géométries, orientations, sols, ...
- analytique : développer des modèles de température de surface prenant en compte la variabilité spatiale et temporelle de la température.
 Disposer d'une
banque de mesures pour validations
Disposer d'une
banque de mesures pour validations Etudier les
phénomènes en jeu
Etudier les
phénomènes en jeu Champ d'investigation :
 Surface à profil
périodique (analogie à un champ
labouré ou à un champ de dunes)
Surface à profil
périodique (analogie à un champ
labouré ou à un champ de dunes) Maquette de dimensions
réduites (portabilité)
Maquette de dimensions
réduites (portabilité) Paramètres
thermo-optiques connus (conductivité thermique, masse
volumique, capacité calorifique,
émissivité)
Paramètres
thermo-optiques connus (conductivité thermique, masse
volumique, capacité calorifique,
émissivité)Contraintes expérimentales :
 Matériau de mise en œuvre
facile
Matériau de mise en œuvre
facile  Forts écarts de
température en surface (mesurables)
Forts écarts de
température en surface (mesurables) Météo bonne
et stable (ciel clair, sans vent, pour limiter les
paramètres extérieurs)
Météo bonne
et stable (ciel clair, sans vent, pour limiter les
paramètres extérieurs)La maquette :
 dimensionnée
avec le code MISTRAL (code de recherche thermique 3D de l'ONERA). Ont
été testés : le matériau,
le profil surfacique, les dimensions,
l'émissivité surfacique, l'orientation cardinale.
Le choix a porté sur une maquette en plâtre, de
profil de surface sinusoïdal, peint en noir, avec les sillons
orientés Nord/Sud, afin que les ombrages solaires creusent
les écarts de température.
dimensionnée
avec le code MISTRAL (code de recherche thermique 3D de l'ONERA). Ont
été testés : le matériau,
le profil surfacique, les dimensions,
l'émissivité surfacique, l'orientation cardinale.
Le choix a porté sur une maquette en plâtre, de
profil de surface sinusoïdal, peint en noir, avec les sillons
orientés Nord/Sud, afin que les ombrages solaires creusent
les écarts de température. 26 thermocouples de type K
coulés dans la masse de la maquette, principalement
à la surface de la crête centrale.
26 thermocouples de type K
coulés dans la masse de la maquette, principalement
à la surface de la crête centrale.
Le dispositif expérimental :
 maquette posée sur des tréteaux à 1 m du sol
maquette posée sur des tréteaux à 1 m du sol station d'acquisition des températures : toutes les 15 minutes
station d'acquisition des températures : toutes les 15 minutes station météo : mesure toutes les mn de :
température et humidité de l'air, vitesse et direction du
vent, rayonnement solaire global
station météo : mesure toutes les mn de :
température et humidité de l'air, vitesse et direction du
vent, rayonnement solaire global caméra IR : images 3 à 4 fois/jour de la surface de la
maquette (vérification d'homogénéité)
caméra IR : images 3 à 4 fois/jour de la surface de la
maquette (vérification d'homogénéité) panneau solaire et batterie : pour rendre le dispositif autonome
panneau solaire et batterie : pour rendre le dispositif autonomeExemple de résultats expérimentaux :
- CORINTHE : maillage surfacique et volumique de la scène à simuler
- DEESSE : calcul des sphères d'éclairement, par appel à MODTRAN (code de transferts atmosphériques)
- TESOS : résolution thermique 1D, 2D ou 3D
- MOLIERE : création d'une image en luminance en entrée capteur
Le module TESOS :
- résolution de l'équation de la chaleur
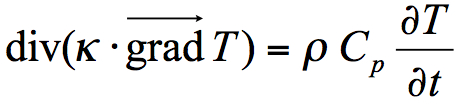 par différences finies
par différences finies - calculs 1D, 2D et 3D
- flux émis :
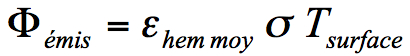
- flux absorbé :
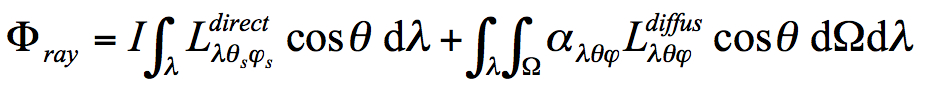

- flux convectif :
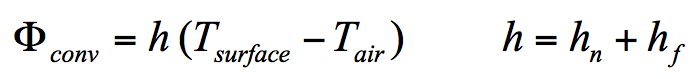
- convection naturelle :
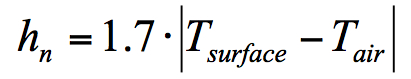
- convection forcée :
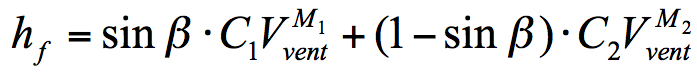
 Améliorations :
Améliorations :- vitesse de vent variable (appel à un fichier météo)
- température d'air variable (modèle analytique de Tair [Jan98], ou appel à un fichier météo)
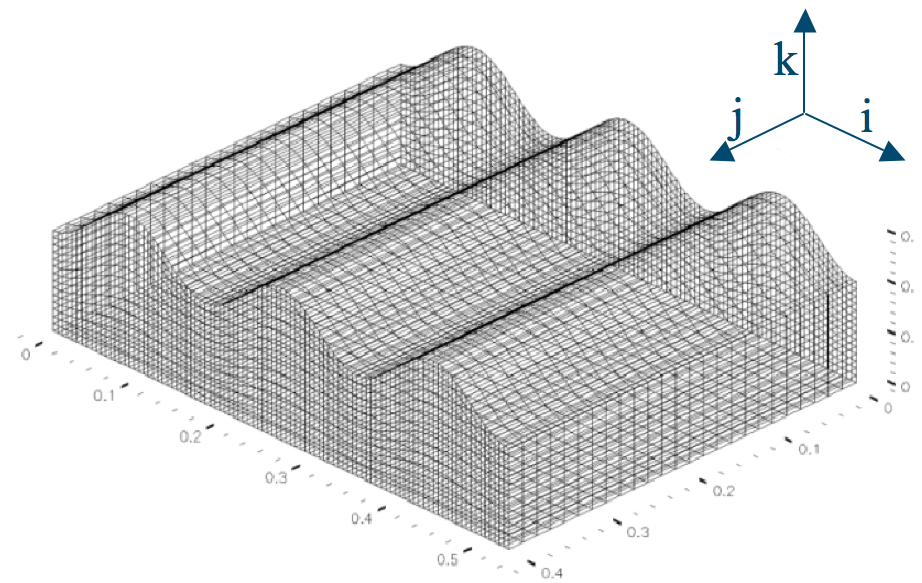
Validation du code MISTRAL :
 Géométrie identique à la maquette Géométrie identique à la maquette Paramètres de calcul (pas de temps, maillage, convergence numérique temporelle) optimaux Paramètres de calcul (pas de temps, maillage, convergence numérique temporelle) optimaux |
 |
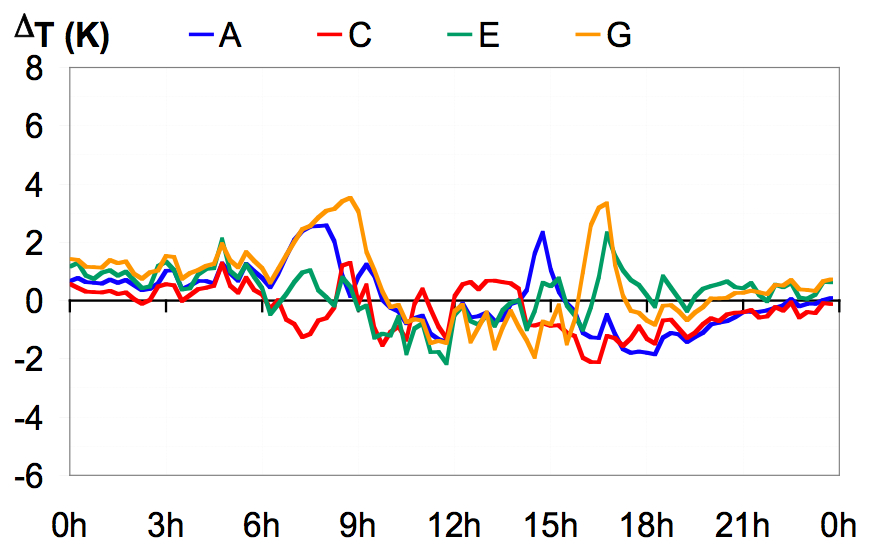
 Comparaison : Comparaison :
|
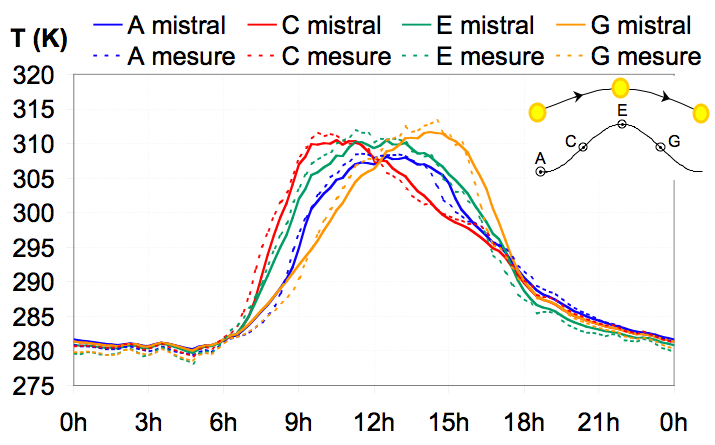  |

